When you first deploy an Exchange Server 2016 database availability group, or any time later when you add a new member to the DAG, there will be some steps required to manage the database copies within the DAG.
As an example, I’ve created a new Exchange 2016 DAG with two members. Before they were added to the DAG the server EX2016SRV1 hosted one database named DB05, and EX2016SRV2 hosted one database named DB06. I’ve then created an additional two databases on EX2016SRV1 named DB07 and DB08. At present the databases have a single copy within the DAG, which looks like this.
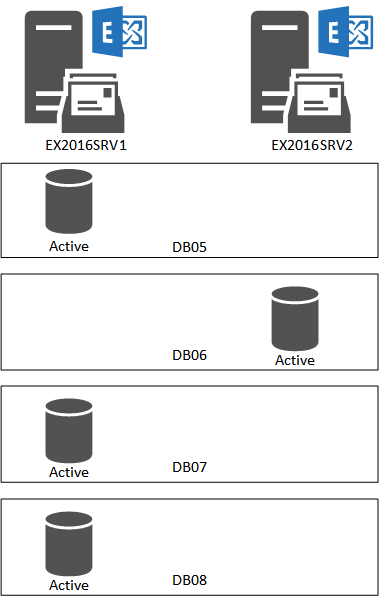
To view this in PowerShell we can run the Get-MailboxDatabaseCopyStatus cmdlet.
[PS] C:\>Get-MailboxDatabaseCopyStatus * | sort name | ft -auto Name Status CopyQueueLength ReplayQueueLength LastInspectedLogTime ContentIndexState ---- ------ --------------- ----------------- -------------------- ----------------- DB05EX2016SRV1 Mounted 0 0 Healthy DB06EX2016SRV2 Mounted 0 0 Healthy DB07EX2016SRV1 Mounted 0 0 Crawling DB08EX2016SRV1 Mounted 0 0 Crawling
In this article I will demonstrate how to:
- Add database copies to a DAG member
- Remove database copies from a DAG member
- Balance active database copies across a DAG
Adding Database Copies to an Exchange Server 2016 DAG Member
The objective in this scenario is to add database copies so that each database has two copies for high availability, one on each DAG member. To achieve this we use the Add-MailboxDatabaseCopy cmdlet. For example, this command will add a copy of DB06 (currently hosted on EX2016SRV2) to the DAG member EX2016SRV1.
[PS] C:\>Add-MailboxDatabaseCopy -Identity DB06 -MailboxServer EX2016SRV1
Adding the new database copy will automatically start the seeding process (copying the database and log files to the new server) and begin the continuous replication process. The new database copy will automatically be configured with the next available activation preference for copies of that database (which I’ll explain later in the section about balancing database copies across a DAG).
The seeding time will depend on the amount of data that needs to be copied and the network bandwidth that is available. The seeding will occur from the database copy that is currently active. If you’re seeding across a slower WAN connection and there is already another passive copy in that datacenter that would be faster to seed from because it is closer, you can modify the command shown above to postpone seeding.
[PS] C:\>Add-MailboxDatabaseCopy -Identity DB06 -MailboxServer EX2016SRV1 -SeedingPostponed
Then, manually start the seeding process using Update-MailboxDatabaseCopy and specify which DAG member to seed from.
[PS] C:\>Update-MailboxDatabaseCopy -Identity DB06EX2016SRV1 -SourceServer EX2016SRV2
You can repeat the commands above to add copies of multiple databases to a new server, however that gets a bit tedious. Instead, we can use PowerShell to add multiple database copies in a single command. For example, here is the list of database copies on EX2016SRV1.
[PS] C:\>Get-MailboxDatabaseCopyStatus -Server EX2016SRV1
Name Status CopyQueue ReplayQueue
Length Length
---- ------ --------- -----------
DB05EX2016SRV1 Mounted 0 0
DB06EX2016SRV1 Healthy 0 0
DB07EX2016SRV1 Mounted 0 0
DB08EX2016SRV1 Mounted 0 0
We know that DB05, DB07, and DB08 are yet to be added to EX2016SRV2. One way to show only the databases in the DAG that are yet to be added to EX2016SRV2 is as follows.
[PS] C:\>Get-MailboxDatabase | Where {$_.MasterServerOrAvailabilityGroup -eq "EX2016DAG01" -and $_.Servers -notcontains "EX2016SRV2"}
Name Server Recovery ReplicationType
---- ------ -------- ---------------
DB05 EX2016SRV1 False None
DB07 EX2016SRV1 False None
DB08 EX2016SRV1 False None
So we can simply pipe that into Add-MailboxDatabaseCopy to add copies to EX2016SRV2.
[PS] C:\>Get-MailboxDatabase | Where {$_.MasterServerOrAvailabilityGroup -eq "EX2016DAG01" -and $_.Servers -notcontains "EX2016SRV2"} | Add-MailboxDatabaseCopy -MailboxServer EX2016SRV2
Run Get-MailboxDatabaseCopyStatus to see the results.
[PS] C:\>Get-MailboxDatabaseCopyStatus * | sort name
Name Status CopyQueue ReplayQueue
Length Length
---- ------ --------- -----------
DB05EX2016SRV1 Mounted 0 0
DB05EX2016SRV2 Healthy 0 0
DB06EX2016SRV1 Healthy 0 0
DB06EX2016SRV2 Mounted 0 0
DB07EX2016SRV1 Mounted 0 0
DB07EX2016SRV2 Healthy 0 0
DB08EX2016SRV1 Mounted 0 0
DB08EX2016SRV2 Healthy 0 0
Removing Database Copies from an Exchange Server 2016 DAG Member
When you are planning to decommission a DAG member you will need to remove all of the database copies from the server before it can be removed from the DAG member list. To remove database copies we use the Remove-MailboxDatabaseCopy.
For example, to remove the copy of DB05 from the DAG member EX2013SRV2 we run this command.
[PS] C:\>Remove-MailboxDatabaseCopy DB05EX2016SRV2 Confirm Are you sure you want to perform this action? Removing database copy for database "DB05" on server "EX2016SRV2". [Y] Yes [A] Yes to All [N] No [L] No to All [?] Help (default is "Y"): y
To remove all of the database copies from a DAG member without being prompted for confirmation use the following command.
[PS] C:\>Get-MailboxDatabaseCopyStatus -Server EX2016SRV2 | Remove-MailboxDatabaseCopy -Confirm:$false
If you try to remove a database copy that is currently active it will fail with an error message similar to this.
The database “DB06” is currently hosted on server “EX2016SRV2”. Use Move-ActiveMailboxDatabase to move the active copy of the database to a different server. You can use the Remove-MailboxDatabase task if this is the only copy.
If you were doing this as part of a server decommission you would simply move the active database copy to another server, then re-run Remove-MailboxDatabaseCopy.
Balancing Active Database Copies for an Exchange Server 2016 DAG
The first copy of a database in a DAG is configured with an activation preference of 1. As you add new copies of that database the copies are configured with activation preference values in order. So the second copy is AP=2, the third is AP=3, and so on. Activation preference and the impact is can have on DAG operations is explained in more detail in my article Why Did My Database Failover to the Wrong Server?
Depending on how you first built your DAG you may have an unbalanced distribution of activation preferences across your database copies. For example in my DAG this is the current layout of the AP values. When all active database copies are the AP=1 copy the DAG will generally function just fine, but the storage IOPS will not be even and it’s possible that some operations such as an unplanned failover may take longer.
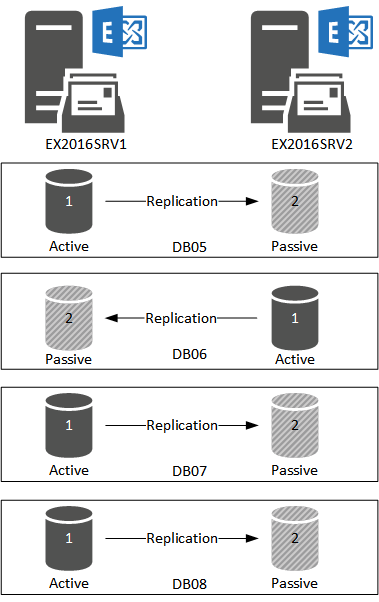
We can balance our activation preferences using some PowerShell scripts, which I’ve previously written about in my article on PowerShell Scripts for Balancing Database Availability Groups. Following the guidance in that article I can run the following command to balance my AP distribution.
[PS] C:\>cd $exscripts [PS] C:\Program Files\Microsoft\Exchange Server\V15\scripts\>.\RedistributeActiveDatabases.ps1 -DagName ex2016dag01 -BalanceActivationPreferences
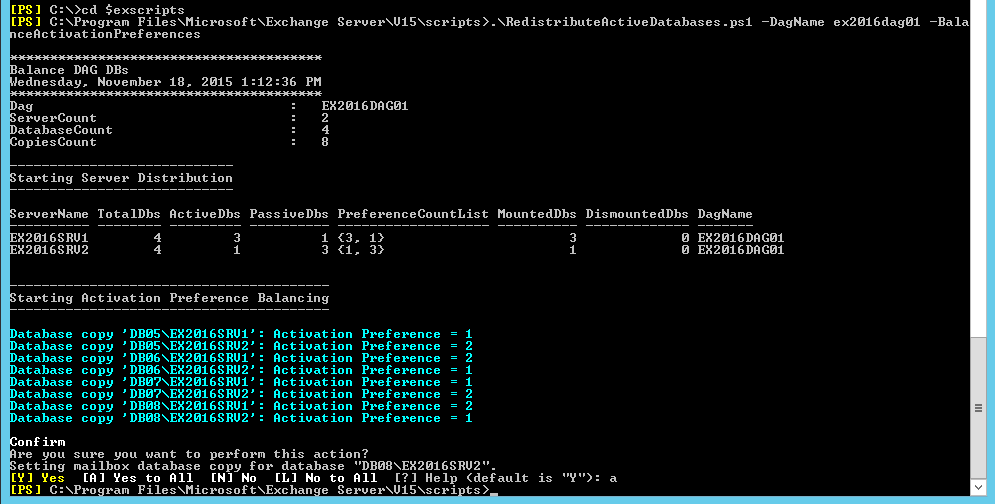
With the AP values more evenly distributed, but now it means some of my active database copies are not the most preferred copy. This in itself is not a problem, but as mentioned earlier a balanced DAG has benefits.
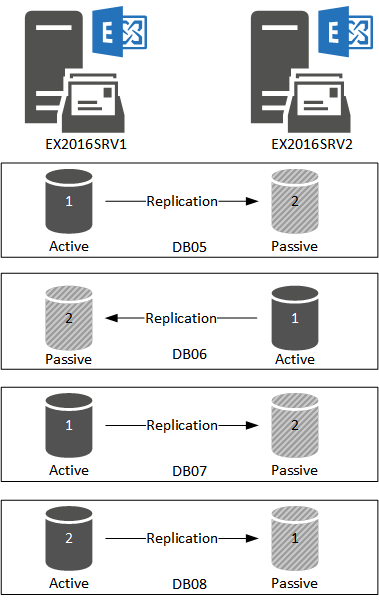
I can rebalance the active database copies with this command.
[PS] C:\Program Files\Microsoft\Exchange Server\V15\scripts\>.\RedistributeActiveDatabases.ps1 -DagName ex2016dag01 -BalanceDbsByActivationPreference -Confirm:$false
Summary
In this tutorial I’ve demonstrated how to add and remove database copies from Exchange Server 2016 database availability group members. I’ve also demonstrated the concept of activation preference, and how to balance activation preferences across your DAG members.
[adrotate banner=”49″]




Hi Paul,
If I have Exchange in C:\ and DB01 in M:\ in serverA, then I use below command to create the database copy.
Add-MailboxDatabaseCopy -Identity DB01 -MailboxServer serverB
Where will the DB01 in serverB be created? in Exchange folder in C:\ or the same path as serverA in M:\?
The Real Person!
Author Tony Redmond acts as a real person and passed all tests against spambots. Anti-Spam by CleanTalk.
It’s a while since I did this, but I believe all the database copies share the same path.
I have inherited a DAG with 2 servers and 1 witness. All the mailbox databases are setup to perform database copies to the opposite server. Our SystemDB on each server (System Databases) are not set to copy. When one of our servers is rebooted, people lose access to their mailboxes. It doesn’t appear that the copies take over when the server is not accessible. Do the System Databases need to be copied to each other? I ran the Test-ReplicationHealth -Identity on my server and it fails at the DatabaseRedundancy check.
Some things to consider:
1) Make sure each Exchange server has a DNS record on your DC. Round robin should be enabled if you do not have a NLB in place
2) You may need to add a firewall NAT rule for each server if you have one for the primary
3) The 2nd dag member should host a passive copy of your db(s). If not you should fix that first.
I currently have 3 DAG members with to large disks, i need te reclaim some free space.
is it possible to remove 1 DAG copy, then delete the large disk.
add a smaller disk and enable the database copy again?
then i just need to repeat this proces 2 more times and i have smaller disks on all my servers.
correct?
Yes, that is exactly what I did and it works fine. If it’s a VM you can start small and always hot add. If your DB is 100GB then I would make a 300GB min partition using the same drive letter as the original. Now you can SEED the db(s).
Hi there
i have just created a DAG on exchange 2016
i only have one exchange server that holds my main database.
i created a 2nd database for the DAG database and i need to replicate the main/active database to my DAG database so if anything happens to my main db, it fails over to the DAG db.
please could you aissist?
thank you
You need to spin up a 2nd Exchange MB server and configure the dag.
Not sure if this is even still being monitored, but…
Is there a way to get all database copies in a 6 member DAG with the lowest activation preference (5) and pipe that into the command to set the lag time for those particular copies?
Hello Paul!
I have a question about using RedistributeActiveDatabases.ps1
I have DAG with 2 servers Exchange 2016. On one server there are 4 active database, on second server there are 4 copy active database.
It is necessary to carry out long-term maintenance work with the first server, at this time the server will be turned off. The work will take about 20 hours. At the time of work to activate all the database on the second server.
What command should be given to move all bases to the second server?
Thanks in advance.
Greetings.
You simply active the passive copies and give it time to switchover. You can do it through ECP or PS.
Paul,
First off, you are the best!
I have 2 servers in a DAG (A and B) with 1 witness server at the same site as A. The servers are behind firewalls with an IPSec tunnel providing private subnet connections. They also have virtual IPs that allow for public internet access. I assume this is a common scenario.
My question is based on a very rare but potential situation. What will happen if the IPSec tunnel were to go down but the WAN connections at each site were to function. In other words, the servers could no longer use their primary method of private subnet communication. They would both be alive and capable of answering requests from the public subnets. Would they both mount their databases or can they determine their status over the internet?
So, if they did both mount the databases is there a recovery method for that after the situation is resolved?
Thank you so much for your website and time!
The Real Person!
Author Paul Cunningham acts as a real person and passed all tests against spambots. Anti-Spam by CleanTalk.
Only one copy of a database can be mounted at any given time.
Some reading for you:
https://www.practical365.com/exchange-server/exchange-best-practices-datacenter-activation-coordination-mode/
https://www.practical365.com/exchange-server/datacenter-activation-coordination-mode/
I am so impressed with your ability to answer all of our redundant questions with professionalism! DAC sounds like the solution!
Thanks!
Good evening Paul,
Should we pre-create the folder structure on the second (or additional) mailbox servers? I know the paths must be identical so I made sure the drive letters were the same (databases on the E: drive and log files on the F: drive). Since I’m only testing Exchange 2016 DAGs at this point, I thought I’d just let Exchange create the folders. Exchange created the folders successfully and all the data replicated correctly. However, there was a warning about folder permissions (slightly edited):
WARNING: There was a problem creating directory “E:\MBXDB-01” on server “EX16-4.my.domain”. In order to ensure that the Exchange data is kept secure, please create the directory, if it does not already exist, and configure directory permissions so that “SYSTEM” and the local “Administrators” group have “Full Control” for the folder, subfolders, and files. It is recomended that permission inheritance be broken so that only “SYSTEM” and “Administrators” have access to the directory.
Once again, that did not prevent the actual creation of another copy of the database.
I was prompted to restart the Information Store service on the second mailbox server (that may be normal).
Test-ReplicationHealth and…
Get-MailboxDatabase | Get-MailboxDatabaseCopyStatus
are both OK.
I notice that on the first server, the permissions on the (manually created) folders are not what is recommended above either (there are additional Exchange groups that have permissions) but I’ll stick with my initial question for now, rather than going all over the place with this.
Thanks in advance!
The Real Person!
Author Paul Cunningham acts as a real person and passed all tests against spambots. Anti-Spam by CleanTalk.
I’ve never pre-created the folders and I’ve never had that error message appear. Perhaps there was an issue with the permissions on the root of the volumes.
David – Were you running the Add-databasecopy cmdlet (or GUI) from the target server? If not, can you delete the DB copy and re-run from the target server?
Good morning, Paul.
As always very good post, I have a question maybe you have already done it but I have not found clear information, I am in process of migration to Exchange 2016, I am thinking of setting up a DAG with 4 servers (2 servers in a central site and 2 servers On a DRP site), I have a question regarding database replication, it is possible in Exchange 2013 or 2016 to replicate a database from a passive copy.
This is because I have a very limited link (8Mb) and I would like to have 1 copy on each server of the remote site and I do not want to replicate 2 times from the central site, I would like to see if it is possible to replicate from a server of the DRP site and thus reduce Network consumption on the WAN.
SitePri Site DRP
Server1 Server2 | Server3 Server4
Active —————> | Pasive1 —> Pasive2
Active–>| Pasive1 —> Pasive2
Thanks in advance.
Greetings.
The Real Person!
Author Paul Cunningham acts as a real person and passed all tests against spambots. Anti-Spam by CleanTalk.
You can do the initial seeding of a database copy from either an active or passive copy, but the ongoing replication is from the active copy only.
Running DAGs over low bandwidth links is not a good idea. If you’re going to do a multi-site DAG, the network has to be good.
I am in the planning stages of upgrading to a Ex2016 standard (2) server DAG plus witness. I am confused about the licensing. Per Microsoft standard allows for 5 mounted DB’s per server whether they are active or passive. So in my case I am planning for 4 active DB’s and a passive copy for each totaling 8. Is my understanding correct or am I missing something? Should I be considering Enterprise instead?
The Real Person!
Author Paul Cunningham acts as a real person and passed all tests against spambots. Anti-Spam by CleanTalk.
Here you go:
https://www.practical365.com/exchange-2016-server-editions-and-licenses/
Short answer, your DAG could have up to 5 databases, with a copy on each DAG member.
Thank you!!