Last week I ran a survey asking about multi-factor authentication (MFA) adoption. Of the hundreds of responses I had actually thought that we would see a clear majority adopting MFA. After all, we all know how important MFA (or 2FA if you prefer) is these days, with high profile breaches of online services causing exposure of usernames and passwords (sometimes encrypted, sometimes not).
Surprisingly, 55% of responses indicated that they do not use MFA at all in their organizations.
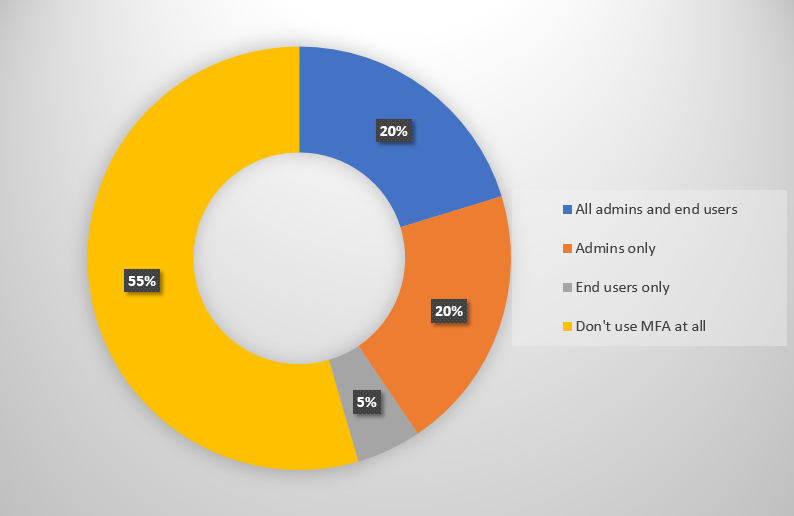
It’s reasonable to assume that some of those 55% are not using any Office 365 or other cloud services at this time. However, due to the make up of the audience that was actually surveyed here, it seems more likely that a good portion of those 55% (not to mention the 20% who say they’re using it for admins only) are using Office 365 in some capacity, have some reservations or obstacles preventing them from rolling out MFA to their user population.
So I’d like to get a discussion going and learn more about those roadblocks that you’re facing. From my own work with customers I know this can be a wide range of technical and political reasons. If you’re not using MFA today, please leave a comment below explaining what has stopped you deploying MFA so far.



Pingback: Multi-factor Authentication by Default for Administrators in Azure AD and Office 365 – SimpleITPro
Can I use MFA with on-premise AD?
You can use Azure MFA (the paid version) to protect some on-premises workloads. See here for a comparison of the different MFA offerings.
https://docs.microsoft.com/en-us/azure/multi-factor-authentication/multi-factor-authentication-versions-plans
As per Conrad. I log in many, many times per day across my tenants – more so if the browsers start to act weird and log you into the wrong tenant or just refuse to log in at all.
Having to type a 6 digit code for each of my tenants, along with the individual codes required for each account would really slow me down. A push notification to my cell for me to say “yep – this is me” might be a better way of doing this.
The ip based bypass would also be very handy.
Do you have to have a higher subscription than the basic E1/E3 or Small Business subscriptions to enabled MFA?
MFA is included with Office 365 for securing O365 apps/services only (e.g. logging into OWA). The feature set of the free offering is basic but it does the job. All the flexibility like IP whitelists is included with Azure MFA, which can be purchased separated or comes bundled with EMS.
I feel a bit bad, but for me it’s a speed thing. Because I am logged in and out of multiple clients, plus our own tenancy so toggling between multiple browsers, incognito and PowerShell gets a bit tricky often having to log and and in several times. The MFA just slows me down. I know it’s probably less than 30 seconds, but in a busy operational and delivery environment that seems ages.
Sounds like an MSP scenario?
Have you considered using Azure MFA with IP-based bypasses?
The challenge we have is the app password. When the user’s open Outlook for example and are prompted for their username and password they put in their domain credentials when Outlook is expecting the app password. Any suggestions on that? If we were just using Office 365 online products we would be golden to push it to our users but the fact that the confusion for the user base occurs we have not been given the go ahead.
What MS don’t tell you in the MFA setup is that by default MFA is not enabled for Exchange Online or Skype for Business, hence why Outlook and SfB both require an AppPassword. You have to enable modern authentication in the Exchange Online tenancy and in the SfB tenancy via Powershell first, then Outlook (and SfB) will happily use the users normal login creds with MFA verification.
This is semi-true. It’s in the deployment guidance but they should definitely make it more obvious in the admin portal when you’re enabling MFA for users.
I find that even with modern authentication enabled the credentials window still pops up from time to time in the morning when you first log in. It eventually stops and stays connected. This is slowing down our deployment especially since MS support does not seem to have an answer for this behavior.
Seems that these days, the user base is a very decisive factor. People (non-admins) do not understand that an environment cannot be safe and simple all the time. User input, and following whats being imposed by admins, is very important to provide a secure and working environment.
Would really like to know how you guys tackle that?
Fair point. Admins and VIPs need to lead the way on this (the most important and powerful accounts should use MFA instead of getting exceptions). It’s also important for even the most low level employee to recognize the value of business information that they can access.
I’ve had some success framing the issue in the context of personal loss. Would you like someone to steal your bank password and take all your money? No, so you should use MFA. Would you like someone to steal your work password and conduct fraud that costs you your job? No, so you should use MFA.
All Office 365 admin’s have it enabled, but as far as end users go, the company culture and user adoption are holding us back from further deploying.
PS was a limiting factor for us too but now we have PS with MFA enabled accounts working there is no excuse (almost).
Really? Is there a guide to enable them? We need to install a module on PS to make it work?
In my recent article here I list the PS modules/connections that currently do and don’t support MFA.
https://www.practical365.com/security/securing-office-365-administrator-accounts-multi-factor-authentication/
Thanks!
How did you get this working, which PowerShell module?
How did you get this working? Which PowerShell module?
Whats stopped me from using it was the lack of PowerShell integration with it.
I know that they recommend to create another user to deal with PowerShell only, but in my organization there are many administrators and we prefer to use our own user because of logging (who did it, when, etc).